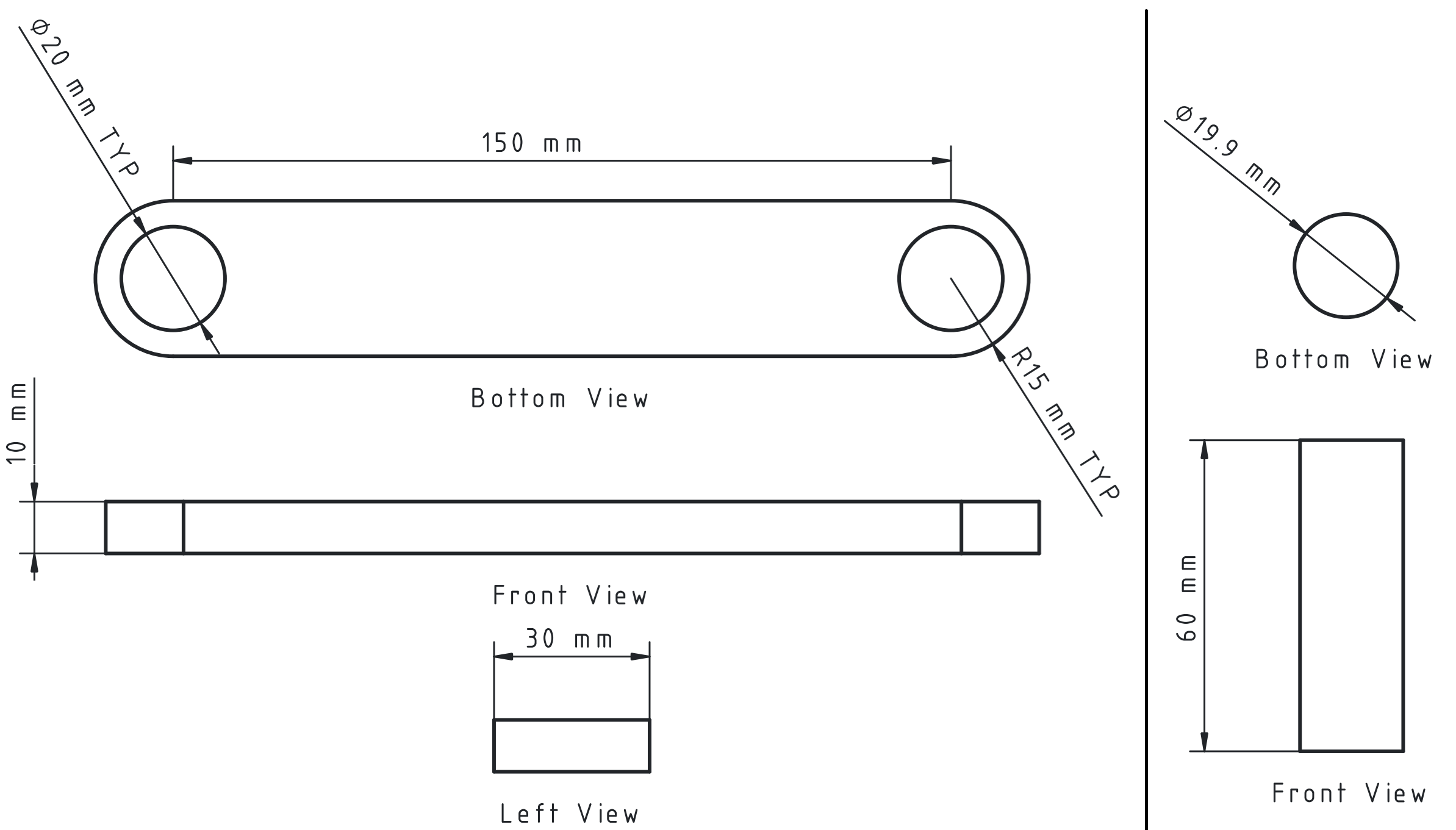
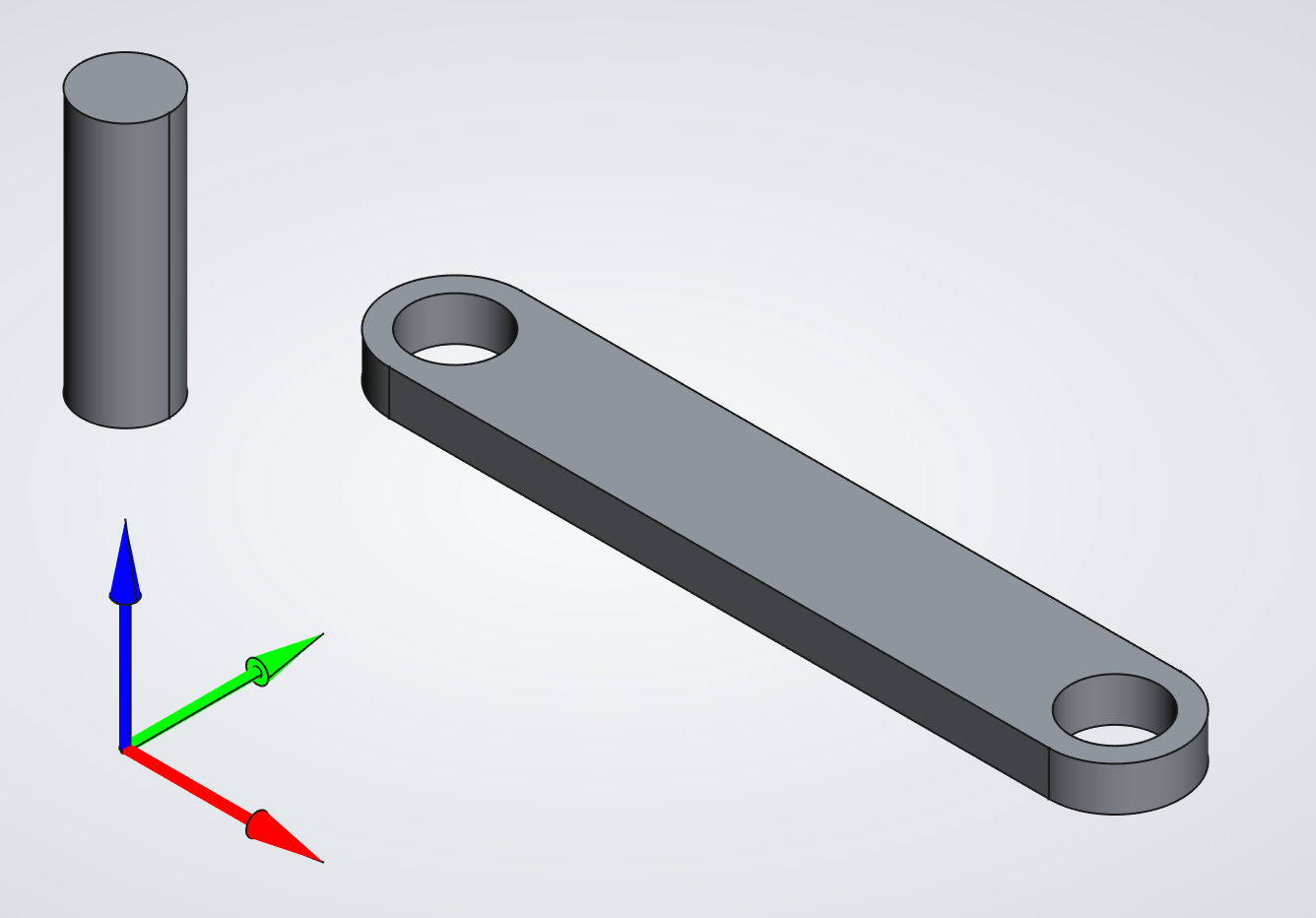
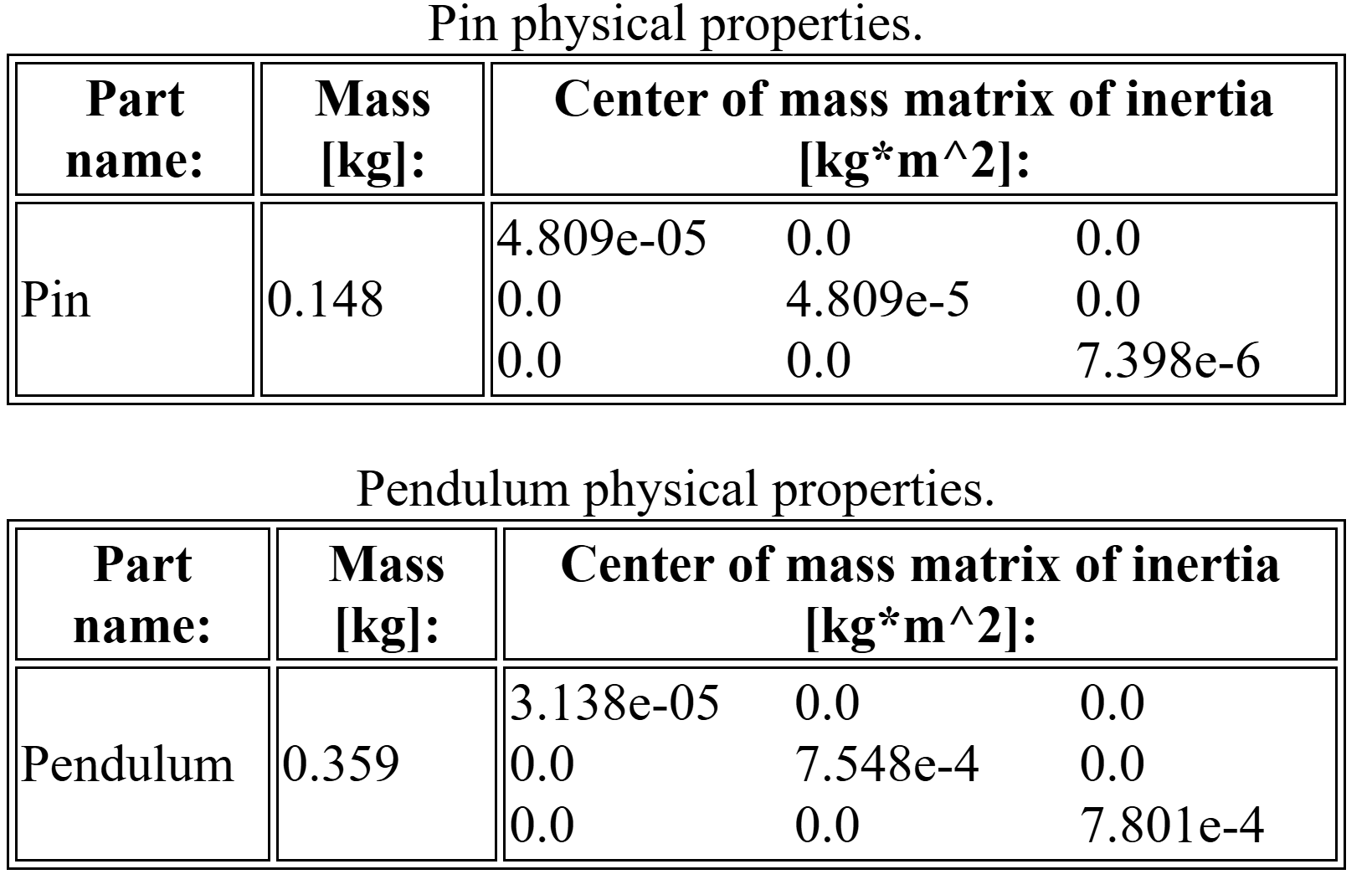
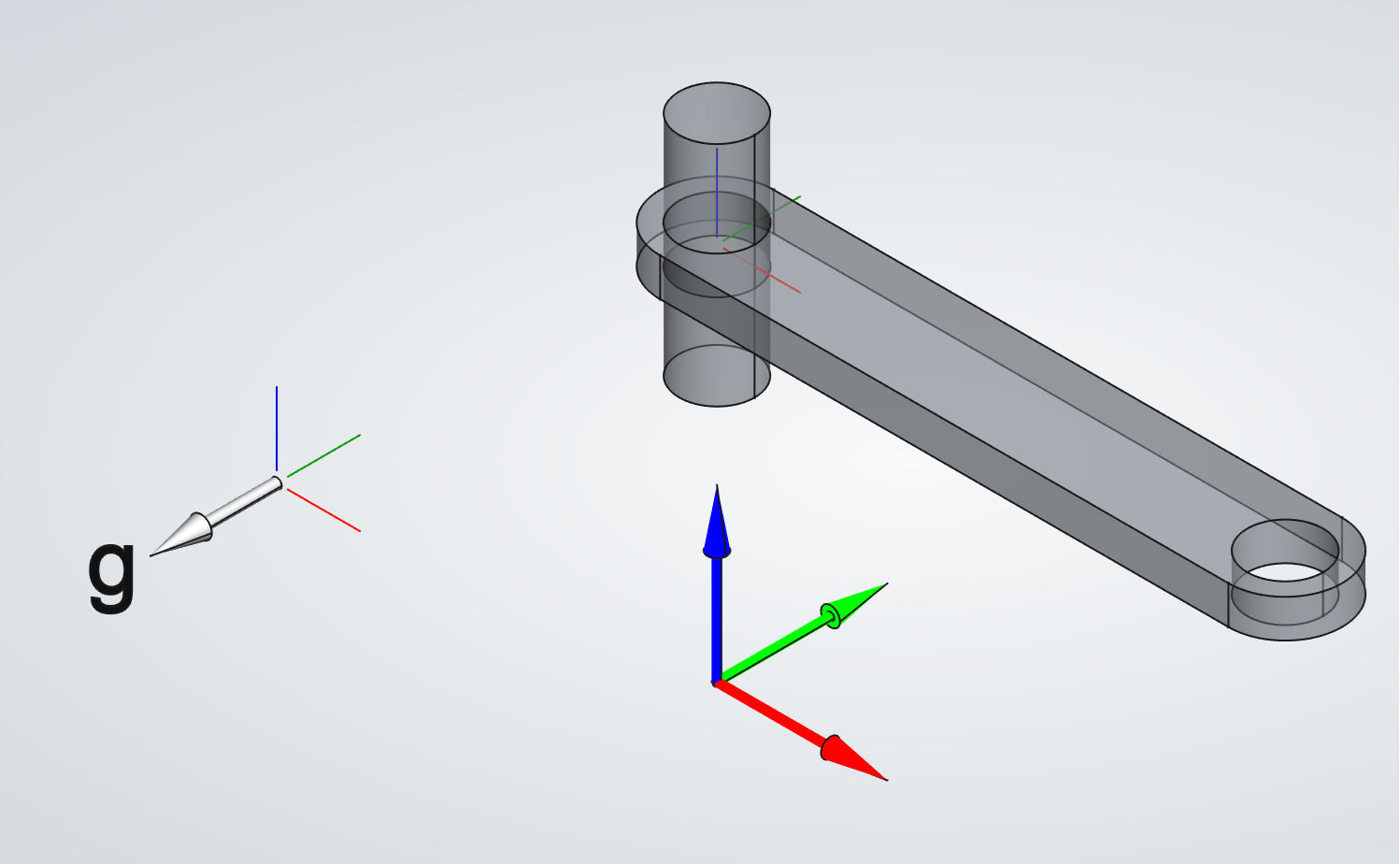
The
d'Alembert principle
ensures the pendulum FEM model is in static equilibrium throughout all the time steps. For this, the total acceleration vector at the
center of mass of each tetrahedron mesh element is computed,
and the negative of this acceleration is applied to each volume element in the FEM mesh.
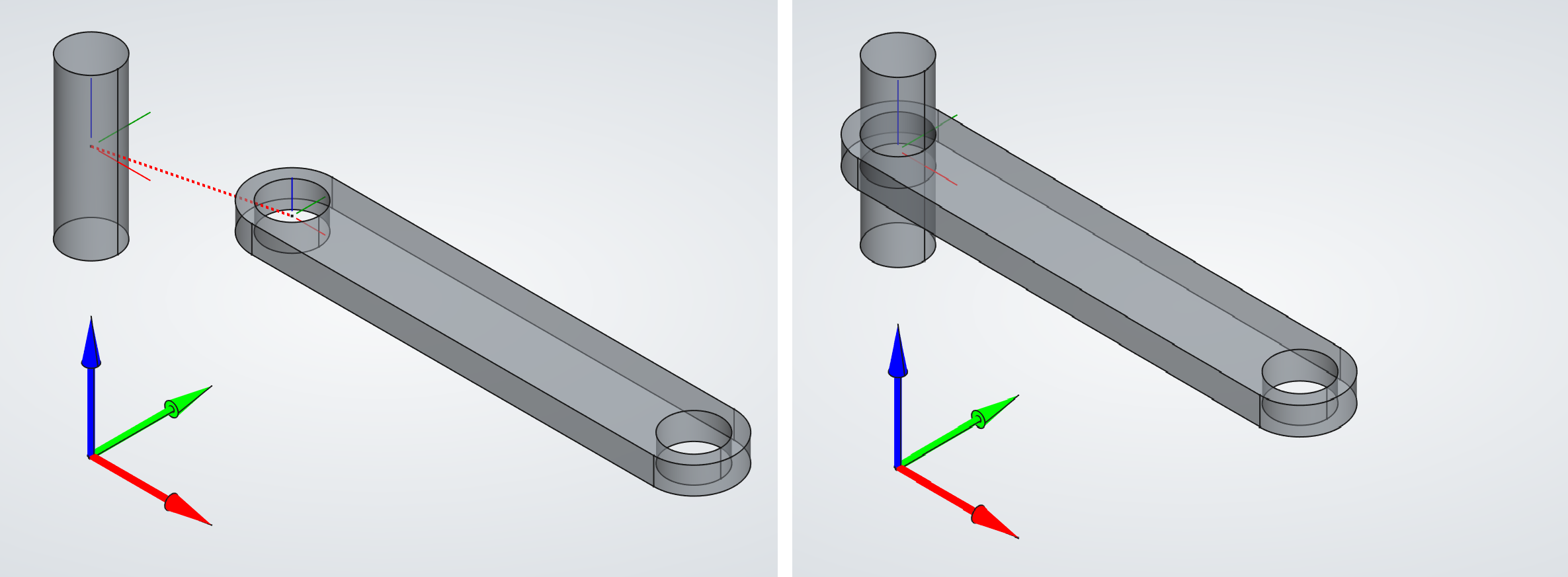
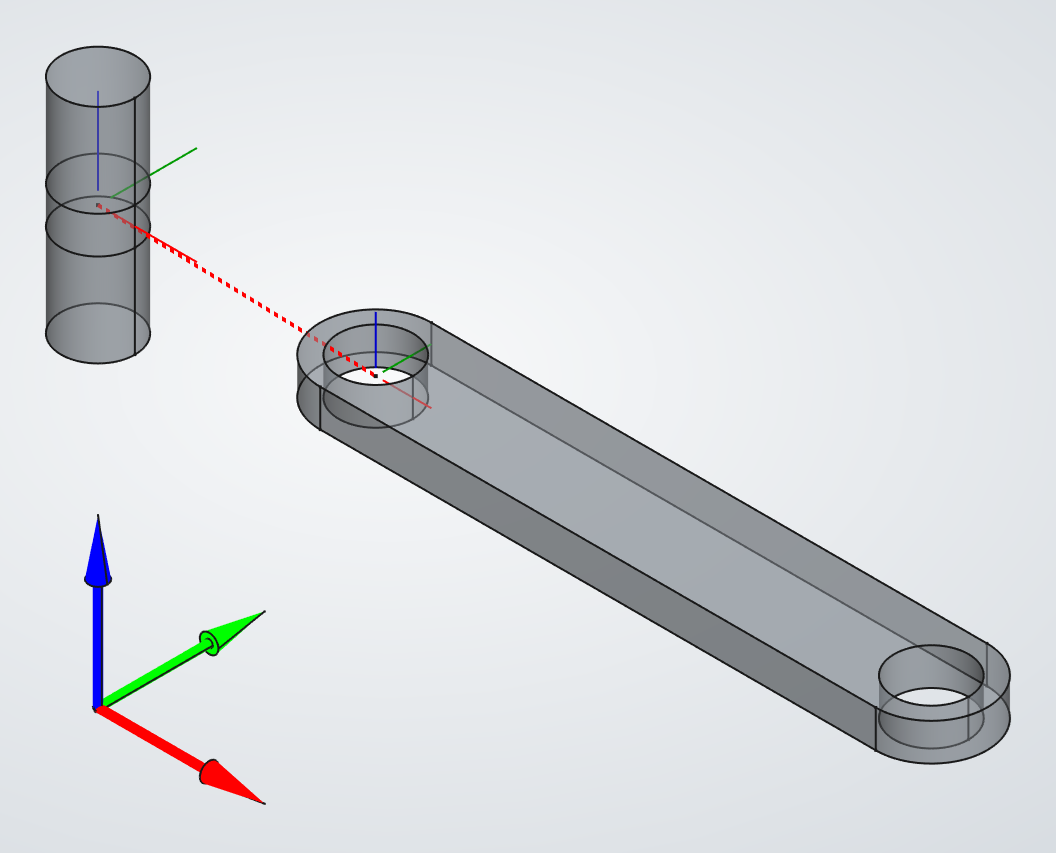
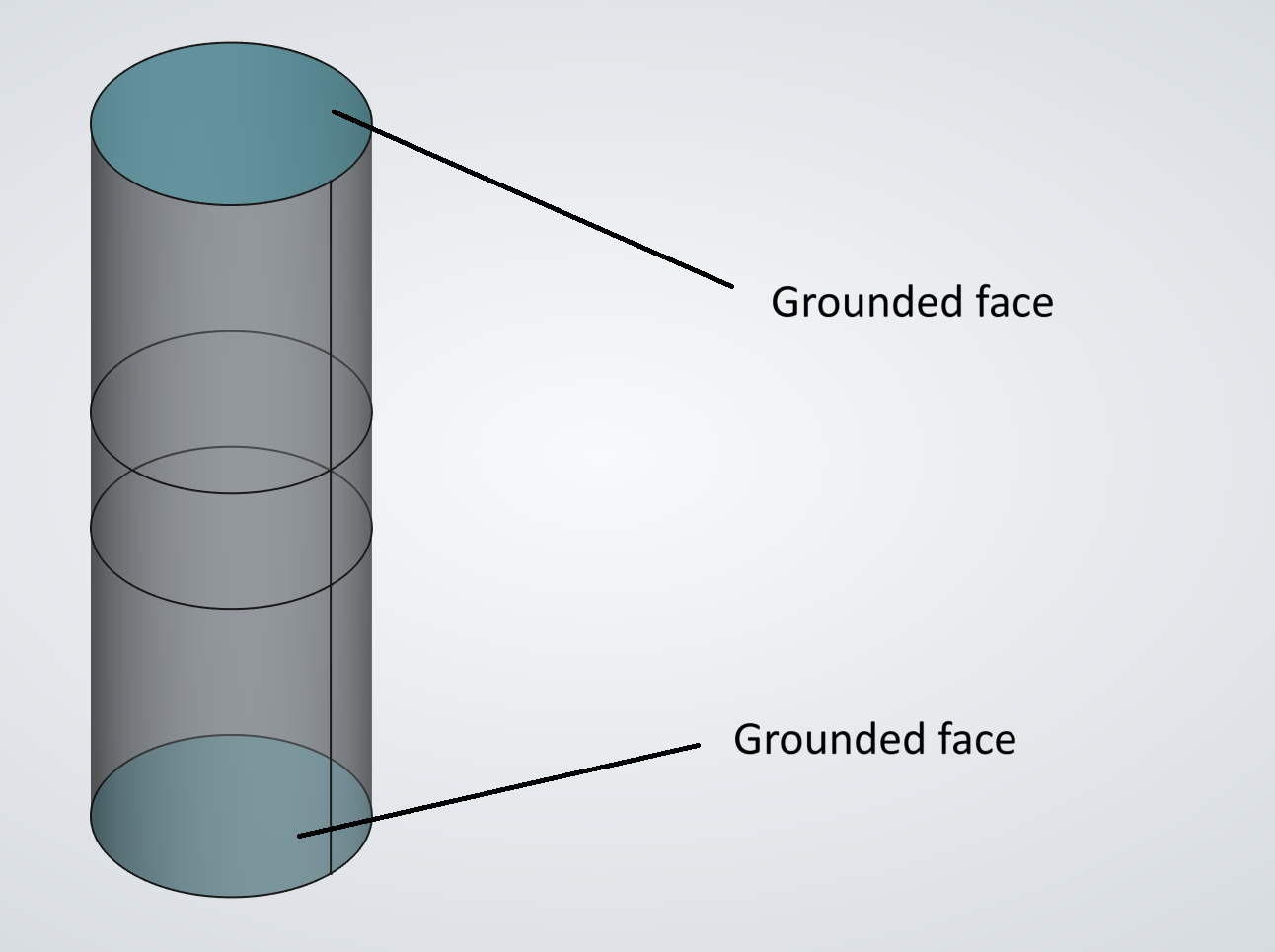
To prevent rigid-body motion, the pre-processor authomatically chooses three suitable nodes and applies fixed boundary conditions
using the "3-2-1" approach.
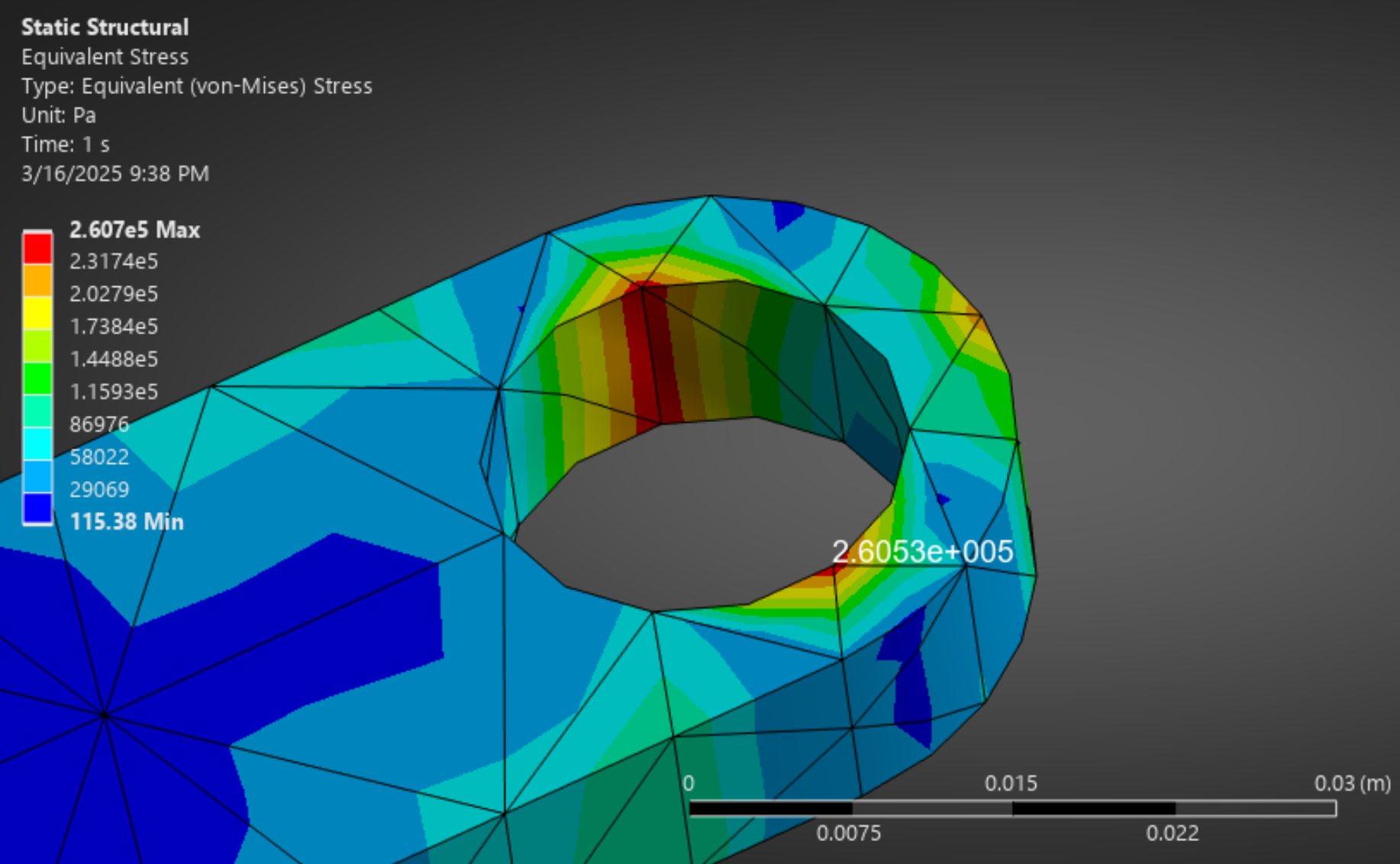
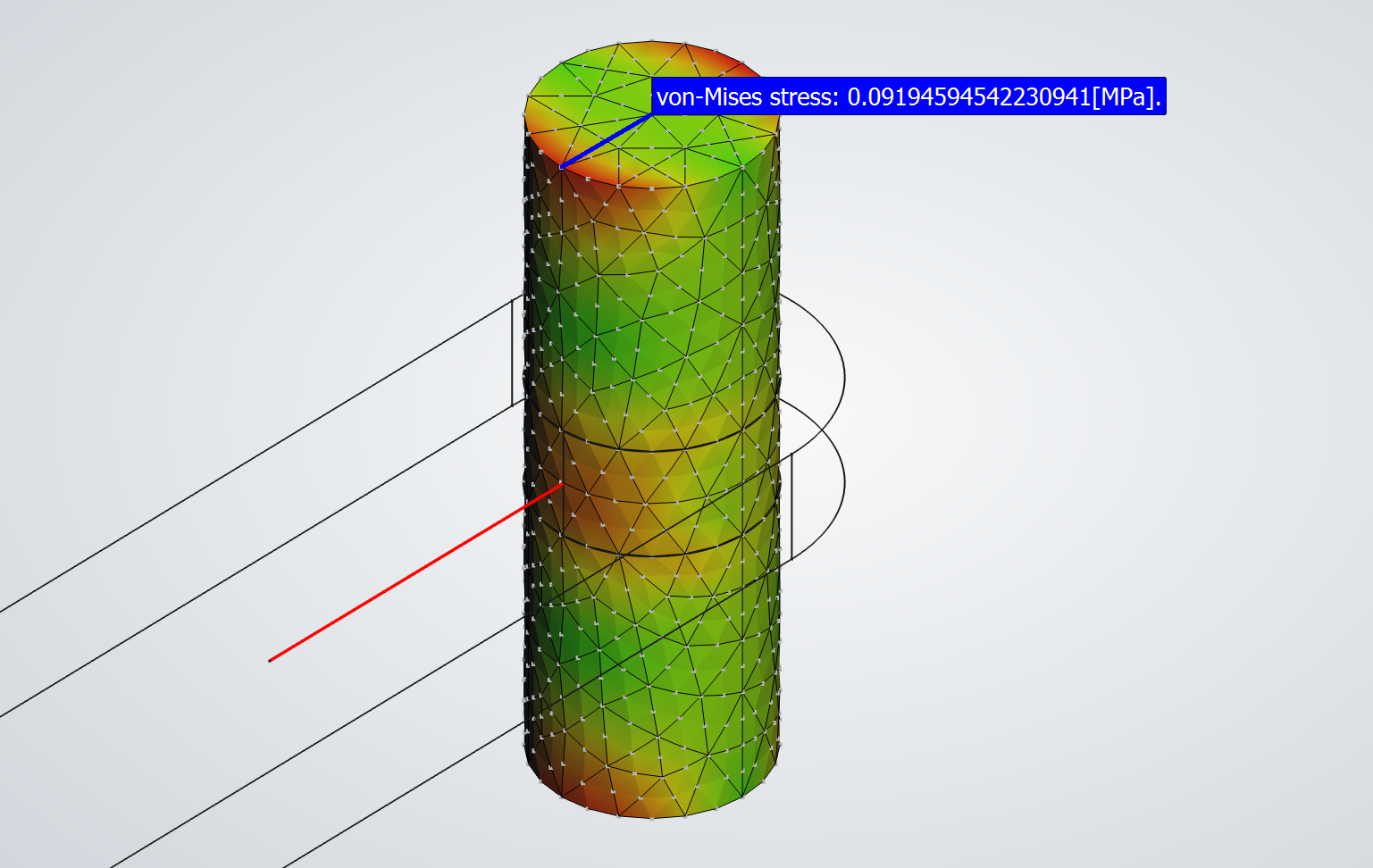
The video on the left shows:
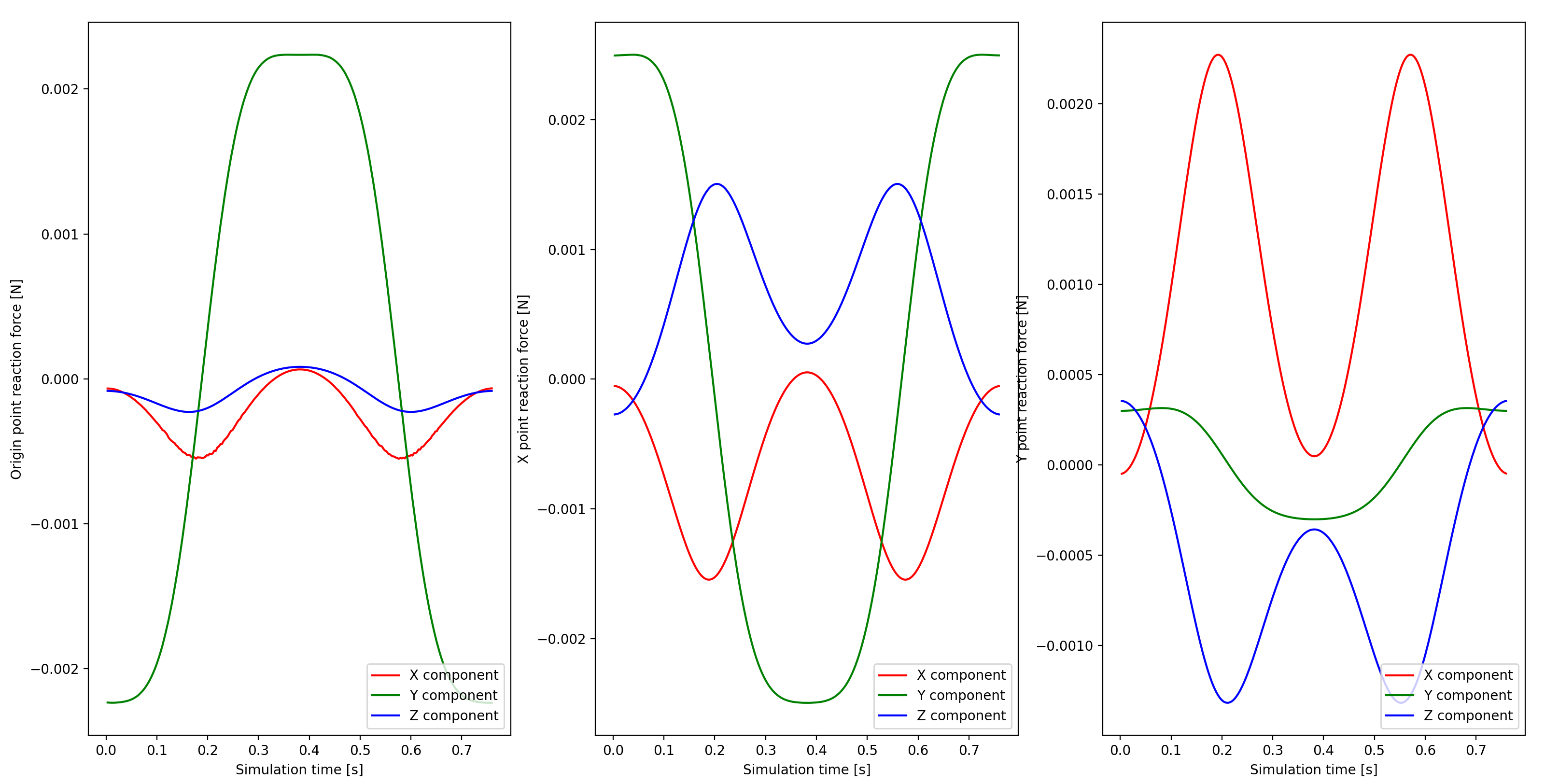
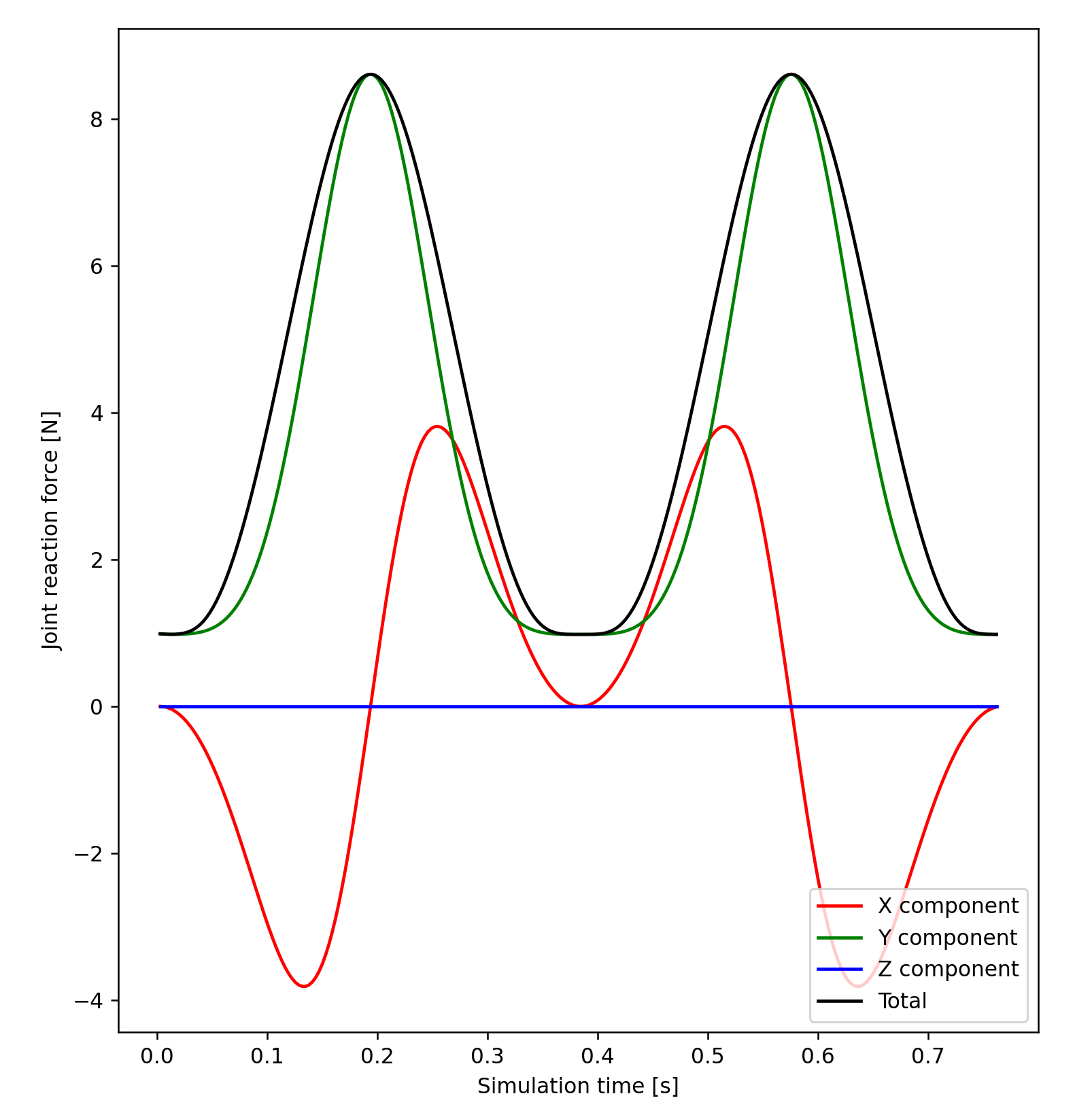
- The joint load distribution among the FEM nodes.
- Gravity and d'Alembert acceleration vectors acting
at the center of mass of an evenly distributed sample of tetrahedron mesh elements.
Load vectors are depicted by red lines. Acceleration vectors in orange.
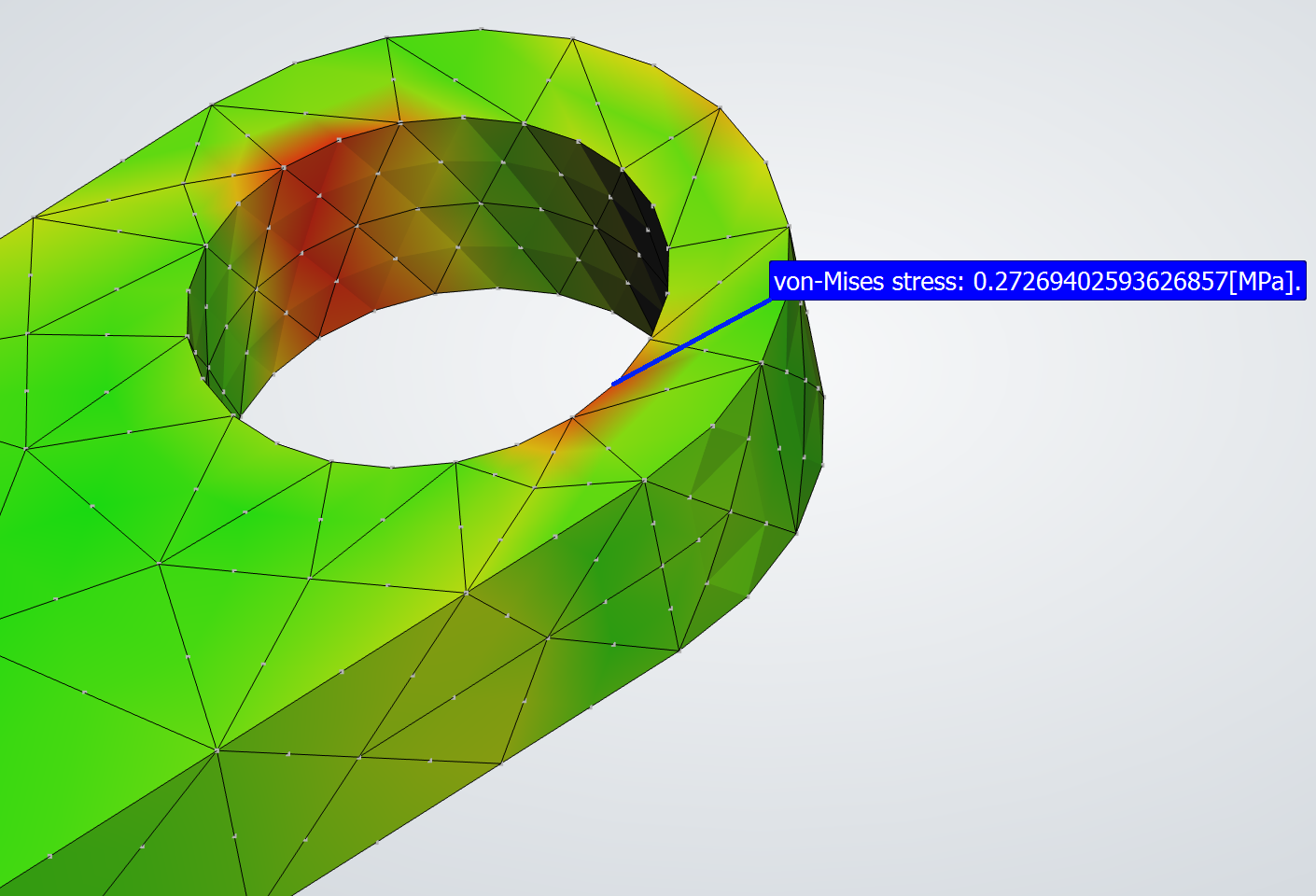
FEM simulation of the pendulum.
The pre-processor generates a set of input files for the FEM solver, one for each time step of the MbD simulation.
These files are in *.inp format.
The FEM solver is launched, solving the set of input files.